Table of contents
- Why Advent of Code
- Solutions
- Day 1: Report RepairDay 1: Report Repair
- Day 2: Password PhilosophyDay 2: Password Philosophy
- Day 3: Toboggan TrajectoryDay 3: Toboggan Trajectory
- Day 4: Passport ProcessingDay 4: Passport Processing
- Day 5: Binary BoardingDay 5: Binary Boarding
- Day 6: Custom CustomsDay 6: Custom Customs
- Day 7: Handy HaversacksDay 7: Handy Haversacks
- Day 8: Handheld HaltingDay 8: Handheld Halting
- Day 9: Encoding ErrorDay 9: Encoding Error
- Day 10: Adapter ArrayDay 10: Adapter Array
- Day 11: Seating SystemDay 11: Seating System
- Day 12: Rain RiskDay 12: Rain Risk
- Day 13: Shuttle SearchDay 13: Shuttle Search
- Day 14: Docking DataDay 14: Docking Data
- Day 15: Rambunctious RecitationDay 15: Rambunctious Recitation
- Day 16: Ticket TranslationDay 16: Ticket Translation
- Day 17: Conway CubesDay 17: Conway Cubes
- Day 18: Operation OrderDay 18: Operation Order
- Day 19: Monster MessagesDay 19: Monster Messages
- Day 20: Jurassic JigsawDay 20: Jurassic Jigsaw
- Day 21: Allergen AssessmentDay 21: Allergen Assessment
- Day 22: Crab CombatDay 22: Crab Combat
- Day 23: Crab CupsDay 23: Crab Cups
- Day 24: Lobby LayoutDay 24: Lobby Layout
- Day 25: Combo BreakerDay 25: Combo Breaker
- Final words
- Footnotes
It is Christmas night, and it is the first time this month that I haven't had to plan my schedule for the evening around a programming puzzle contest. For the last 25 days this month, I participated in Advent of Code 2020, and I managed to collect all 50 stars!

I solved all the puzzles in the Julia programming language, and my solutions are available here.
In this post, I wanted to share why I think you should do Advent of Code and idiomatic solutions to all 25 days in the Julia programming language.
Why Advent of Code
Advent of Code is a lot of fun. I think there's a few reasons I find it quite enjoyable.
Firstly, there's the competitive aspect of it.
A single puzzle unlocks every night at midnight Eastern Time, and the time when you submit a solution is recorded. There's a global leaderboard that highlights the top 100 fastest times but you also have the ability to make a private leaderboard that you can share with anyone you like, and you can use that to track your time and challenge your friends or peers.
For straightforward puzzles, it is a lot of fun to see who can read, grok and type out a bug-free working program the fastest. A bunch of people also upload recordings of their attempts, and it is humbling to see how fast they can whip out a correct solution to a problem.
Secondly, unlike most other competitive programming challenges, the puzzles are mainly designed to be a teaching / learning experience.
Every puzzle has two parts, where the first part introduces a prompt, and requires you to solve it before viewing the second part. The first part tends to set up an idea or check that you are on the right track, and the second part tends to extend the idea or subvert an obvious decision you made in the first part.
Almost all the problems require parsing text input of various formats. In some of the latter puzzles, the puzzle inputs may be designed to hedge against certain naive solutions. Some puzzle inputs will only work with certain data structures or certain algorithms. There are a lot of "ah ha" moments when you figure what you should use and when, which makes for a very satisfying solve.
Most problems are based on standard computer science programming concepts, but are never presented as such. Some problems have a mathematics tilt to it, which can make finding those solutions quite rewarding. But also, every problem is designed such that even if you don't know the "theory" behind it you'll be able to stumble your way into solving it if you persevere. Reading other people's one liners after you hacked it together is quite enlightening.
And since various programming language communities discuss their solutions in dedicated forums, there tends to be a lot of discussion about the tips and tricks you can use in your favourite programming language to express the problem more elegantly. Even after having used Python and Julia for years now, I still learn new things when I read other people's solutions.
And finally, that brings me to the community.
The /r/adventofcode subreddit and the Julia Zulip and Slack channel have been a joy to visit every day after solving the puzzles. I've particularly enjoyed seeing all the neat visualizations that come out of Advent of Code by the community.
That's the really neat thing about Advent of Code. The problems are short enough to be solved in less than an hour, the solutions are small enough to be written in just one file, puzzles tend to tackle just one concept or idea, and there is a large enough community around it. Consequently, a lot of people tend to share their solutions, and you get to see a lot of discussion around each puzzle, including a number of different ways to approach the same problem.
If you've never heard of Advent of Code, I highly recommend you try it out. Below I'll be discussing solutions in Julia that were shared on Zulip, Slack and Reddit. This will contain spoilers for all days in Advent of Code 2020.
Solutions
- Report Repair
- Password Philosophy
- Toboggan Trajectory
- Passport Processing
- Binary Boarding
- Custom Customs
- Handy Haversacks
- Handheld Halting
- Encoding Error
- Adapter Array
- Seating System
- Rain Risk
- Shuttle Search
- Docking Data
- Rambunctious Recitation
- Ticket Translation
- Conway Cubes
- Operation Order
- Monster Messages
- Jurassic Jigsaw
- Allergen Assessment
- Crab Combat
- Crab Cups
- Lobby Layout
- Combo Breaker
Day 1: Report Repair
Day 1 of advent of code is basically intended to check that you have a programming language
installed, and you know how to use simple features it in (e.g. for loops).
You can solve the first day with just multiple for loops. However, a more idiomatic solution can
be expressed using the combinations function from the
Combinatorics.jl1:
using Combinatorics
readInput() = sort(parse.(Int, split(strip(read(joinpath(@__DIR__, "./input.txt"), String)))))
expense_report(data, n) = only(prod(items) for items in combinations(data, n) if sum(items) == 2020)
part1(data = readInput()) = expense_report(data, 2)part2(data = readInput()) = expense_report(data, 3)In Julia, small functions are usually made into their single line form. Here's how you would write it if you would like to do it in the multi-line form.
function part1(data = readInput()) expense_report(data, 2)endFunctions also implicitly return the last expression evaluated as part of the function body, if an
explicit return is not present.
Day 2: Password Philosophy
Day 2 is a simple case of parsing, counting characters in a string and knowing that "exactly one"
can be expressed using the xor operation.
The solution below is based on Sukera's.
readInput() = split(strip(read(joinpath(@__DIR__, "./input.txt"), String)), '\n')
function parseInput(data) d = split.(data, ": ") map(d) do (policy,password) rule, letter = split(policy, ' ') low, high = parse.(Int, split(rule, '-')) (low, high, only(letter), strip(password)) endend
function part1(data = readInput()) count(parseInput(data)) do (low, high, letter, password) low <= count(==(letter), password) <= high endend
function part2(data = readInput()) count(parseInput(data)) do (low, high, letter, password) (password[low] == letter) ⊻ (password[high] == letter) endendJulia supports an infix operator for xor: ⊻.
If a function f takes another function as the first argument, you can use the f(c) do ... end
block syntax to map over every element in the collection c and apply the anonymous function
defined by the do ... end block, the result of which is processed by the function f.
For example, if you would like to do the following:
julia> is_a(letter) = letter == "a"
julia> count(is_a, ["a", "b", "c"])1you can express it like so instead:
julia> count(["a", "b", "c"]) do letter letter == "a"end1Alternatively, you can pass in an anonymous function as the first argument by using the thin arrow
->:
julia> count(letter -> letter == "a", ["a", "b", "c"])1In Julia, you can use the only function to get the one and only element in a collection.
julia> only("h")'h': ASCII/Unicode U+0068 (category Ll: Letter, lowercase)Day 3: Toboggan Trajectory
A lot of advent of code problems have the puzzle input as text that represents a grid. Day 3 is our first introduction to a grid of trees.
Having a one liner to convert the text input to a Matrix can be very useful.
readInput() = permutedims(reduce(hcat, collect.(readlines(joinpath(@__DIR__, "./input.txt")))))Here's what the input for this particular day looks like:
julia> A = readInput();
julia> typeof(A)Matrix{Char} (alias for Array{Char, 2})
julia> size(A)(323, 31)
julia> xy = findall(==('#'), A);
julia> using SparseArrays; sparse([p.I[1] for p in xy], [p.I[2] for p in xy], [1 for _ in xy])323×31 SparseMatrixCSC{Int64, Int64} with 2611 stored entries:⠟⣿⡿⡯⣮⣿⡇⡗⣿⣿⢿⢝⣽⡇⡞⡾⣟⢏⣭⢯⡂⣷⣿⣿⢽⣟⣻⠇⢺⣯⣗⠽⣟⣿⡂⡬⡻⡯⡿⣯⣵⡇⠾⣟⣿⡺⣽⣫⠅⣿⡿⡏⣯⡈⣻⠅⢫⢯⣿⣻⡻⡏⡁⠭⡟⣻⡿⢽⣿⠇⣝⣽⣷⡑⣟⢽⠇⢗⣛⣱⣝⠯⡟⡇⣌⣷⡛⢯⣿⡗⠇⢷⠿⡍⢶⡯⣟⡅⡝⣿⡻⣿⣿⢿⡂⢜⠽⢯⣿⣻⣇⠁⠹⢿⢻⡯⡟⡛⡅⣷⣮⣽⣿⡿⡻⡃⣻⡯⣞⣷⣿⡏⠆⣮⡗⣟⢫⣵⣿⡆⣌⣶⣾⣢⣿⣷⡅⣜⡷⡿⠷⣿⣛⡁⣶⣽⣮⣾⣏⡋⡅⣭⣽⣃⣧⣾⣳⡃⣟⣿⡿⣯⣿⡽⡀⣼⣪⣗⣯⡖⡿⡃⣯⢿⡹⣻⣯⣇⡇⣵⣟⡝⢾⢽⣳⠅⡿⣯⡿⣻⣿⣿⡃⣇⣿⣟⣶⣿⣦⡇⡺⣝⣷⣎⢟⣛⡅⣻⢏⣯⣟⣎⣓⡅⡕⣿⣿⣵⣕⢽⡇⡿⣟⣿⣮⣯⣷⡃⣟⡃⣇⡻⣿⣯⡇⣠⣧⣾⣟⣞⢿⠀This solution is based on Henrique Ferrolho's solution.
function solve(trees, slope) n = cld(size(trees, 1), slope.y) rs = range(1, step=slope.y, length=n) cs = range(1, step=slope.x, length=n) cs = map(c -> mod1(c, size(trees, 2)), cs) idxs = CartesianIndex.(rs, cs) count(==('#'), trees[idxs])end
part1(data = readInput()) = solve(data, (x = 3, y = 1))part2(data = readInput()) = prod(solve.(Ref(data), [(x=1,y=1),(x=5,y=1),(x=3,y=1),(x=7,y=1),(x=1,y=2)]))In Julia, you ==(e) returns a "fixed" function which partially applies over the value of e and
accepts one argument which you can use to test equality.
julia> ==('#')('#')true
julia> ==('#')('.')falseJulia has mod1 for 1 based mod, which is useful for indexing in these type of situations. Julia
also has ceiling division (cld) and floor division (fld) which happen to be handy here.
Julia has support for broadcasting using the f.(c) syntax, which allows for the element by element
application of the method f on every element in the collection c, i.e. f(e) for e in c. This
tends to be very handy in Advent of Code.
julia> c = [1, 2, 3, 4, 5];
julia> f(x::Int) = x + 1;
julia> println(f.(c))[2, 3, 4, 5, 6]Additionally, you can use Ref(data) to tell Julia that it is a singleton that shouldn't be
broadcast over. Alternatively, you can use (data,) to get the same behavior.
Day 4: Passport Processing
Since the input has passports separated by an empty line, you can split on "\n\n" to get each
passport into an element of a Vector.
readInput() = split(read(joinpath(@__DIR__, "./input.txt"), String), "\n\n")This is what the first 5 passports look like:
julia> readInput() |> x -> first(x, 3)5-element Vector{SubString{String}}: "hgt:159cm\npid:561068005 eyr:2025 iyr:2017 cid:139 ecl:blu hcl:#ceb3a1\nbyr:1940" "iyr:2014\nbyr:1986 pid:960679613 eyr:2025 ecl:hzl" "cid:211 ecl:blu hcl:#7d3b0c iyr:2011 pid:006632702\nbyr:1982 eyr:2023 hgt:68in"Julia allows piping the results of one function into another using |>.
Learning how to use regex well in your programming language of choice can make solutions concise and terse. Check out this solution by Pablo Zubieta:
const fields1 = (r"byr", r"iyr", r"eyr", r"hgt", r"hcl", r"ecl", r"pid")const fields2 = ( r"byr:(19[2-9][0-9]|200[0-2])\b", r"iyr:20(1[0-9]|20)\b", r"eyr:20(2[0-9]|30)\b", r"hgt:(1([5-8][0-9]|9[0-3])cm|(59|6[0-9]|7[0-6])in)\b", r"hcl:#[0-9a-f]{6}\b", r"ecl:(amb|blu|brn|gry|grn|hzl|oth)\b", r"pid:\d{9}\b")
part1(data = readInput()) = count(p -> all(t -> contains(p, t), fields1), data)part2(data = readInput()) = count(p -> all(t -> contains(p, t), fields2), data)There were a lot of puzzles this year where I would have been able to parse the input more easily by knowing just a little bit more regex.
Day 5: Binary Boarding
Sometimes having a little insight into what the problem is asking can go a long way. For example, in this puzzle, the seat ID is just a binary representation of the input.
So you can calculate the seat ID using binary shifting or by converting the input to 1s and 0s
and parsing the input as a binary number directly.
This solution is based on Andrey Oskin's:
seatid(s) = reduce((x, y) -> (x << 1) | ((y == 'R') | (y == 'B')), s; init = 0)# ORseatid(s) = parse(Int, map(c -> c ∈ ('R', 'B') ? '1' : '0', s), base = 2)
part1() = mapreduce(seatid, max, eachline(joinpath(@__DIR__, "./input.txt")))
function part2() seats = sort(seatid.(eachline(joinpath(@__DIR__, "./input.txt")))) prev = first(seats) for seat in seats (seat - prev == 2) && return prev + 1 prev = seat endendThe eachline function is an alternative to readlines. It iteratively reads from a stream or IO.
Day 6: Custom Customs
Day 6 introduces set operations with the prompt asking you to identify "any" and "every" question,
which can be expressed using union and intersect.
readInput() = split.(split(read(joinpath(@__DIR__, "./input.txt"), String), "\n\n"))
part1(data = readInput()) = sum(q -> length(∪(Set.(q)...)), data)part2(data = readInput()) = sum(q -> length(∩(Set.(q)...)), data)In Julia, you can use the unicode symbols of mathematical operations for union and intersect of
sets, namely ∪ and ∩ respectively. In the Julia REPL or text editors with Julia plugins, you can
use the \LaTeX name and tab complete to get the unicode symbol.
julia> \cup<TAB>
julia> ∪union (generic function with 5 methods)
julia> \cap<TAB>
julia> ∩intersect (generic function with 19 methods)Also, julia has methods on functions like sum that accept a function as the first argument, which
is useful for mapping over every element in a collection.
The ... operator can be used to splat elements from a collection into arguments of a function.
julia> f(a, b, c) = @show a, b, c;
julia> x = [1, 2, 3];
julia> f(x...);(a, b, c) = (1, 2, 3)Day 7: Handy Haversacks
Day 7 is the first introduction to graphs this year. While it is possible to find solutions to both parts of this puzzle using recursion, the problem can be well represented as a graph.
This code is based on Ali Hamed Moosavian's and Andrey Oskin's solutions and visualizations:
using LightGraphsusing SimpleWeightedGraphs
readInput() = build_graph(split(strip(read(joinpath(@__DIR__, "./input.txt"), String)), '\n'))
function build_graph(data) edges = [] for line in data outer_bag, inner_bags = split(line, " contain ") occursin("no other bags", inner_bags) && continue for bag in split(inner_bags, ", ") counter, name = parse(Int, first(bag)), strip(bag[3:end], '.') e = String(rstrip(outer_bag, 's')), String(rstrip(name, 's')), counter push!(edges, e) end end
nodes = collect(Set(src for (src, _, _) in edges) ∪ Set(dst for (_, dst, _) in edges)) mapping = Dict(n => i for (i,n) in enumerate(nodes))
g = SimpleWeightedDiGraph(length(nodes)) for (src, dst, counter) in edges add_edge!(g, mapping[src], mapping[dst], counter) end g, mapping, nodesendNow that you have built a graph, you can find the solution by just traversing the graph.
part1(data = readInput()) = part1(data[1], data[2])part1(g, mapping) = count(!=(0), bfs_parents(g, mapping["shiny gold bag"], dir = :in)) - 1
function total_bags(g, v) isempty(neighbors(g, v)) && return 1 1 + sum(neighbors(g, v)) do nb Int(g.weights[nb, v]) * total_bags(g, nb) endend
part2(data = readInput()) = part2(data[1], data[2])part2(g, mapping) = total_bags(g, mapping["shiny gold bag"]) - 1

Julia allows for multiple dispatch based on the number of arguments and the type of each argument. This lets you define multiple methods of a function.
Day 8: Handheld Halting
Day 8 appears to be a straightforward op code interpreter.
readInput() = strip(read(joinpath(@__DIR__, "./input.txt"), String))
part1(data = readInput()) = boot(split(data, '\n'))part2(data = readInput()) = corrupt(split(data, '\n'))
function boot(instructions) acc, i, s = 0, 1, Set{Int}() while true i ∈ s ? break : push!(s, i) inst, n = split(instructions[i]) n = parse(Int, n) inst == "acc" && ( i += 1; acc += n ) inst == "jmp" && ( i += n ) inst == "nop" && ( i += 1 ) end accend
function corrupt(original_instructions) for j in 1:length(original_instructions) boot_loop_detected = false acc, i, s = 0, 1, Set{Int}() instructions = copy(original_instructions) if occursin("jmp", instructions[j]) instructions[j] = replace(instructions[j], "jmp" => "nop") elseif occursin("nop", instructions[j]) instructions[j] = replace(instructions[j], "nop" => "jmp") end while true i ∈ s ? ( boot_loop_detected = true; break ) : push!(s, i) i > length(instructions) && break inst, n = split(instructions[i]) n = parse(Int, n) inst == "acc" && ( i += 1; acc += n ) inst == "jmp" && ( i += n ) inst == "nop" && ( i += 1 ) end !boot_loop_detected && return acc endendI believe this problem can also be represented as a graph and solved using memoized depth first
search. I would like to re-write this solution using
LightGraphs.jl.
Day 9: Encoding Error
Day 9 was also straightforward.
readInput() = parse.(Int, split(strip(read(joinpath(@__DIR__, "./input.txt"), String)), '\n'))
function check(numbers, n) for i in numbers, j in numbers i + j == n && return true end falseend
function part1(numbers = readInput()) preamble = 25 for i in (preamble + 1):length(numbers) check(numbers[i-preamble:i-1], numbers[i]) && continue return i, numbers[i] endend
function part2(numbers = readInput()) idx, num = part1(numbers) for i in eachindex(numbers), j in i:lastindex(numbers) sum(numbers[i:j]) == num && return sum(extrema(numbers[i:j])) endendJulia has a function called extrema that computes the minimum and maximum element in a single
pass.
julia> extrema([1,2,3,4,5])(1, 5)Teo ShaoWei's solution using Combinatorics.jl is also quite elegant.
using Combinatorics
readInput() = parse.(Int, split(strip(read(joinpath(@__DIR__, "./input.txt"), String)), '\n'))
function bad_number(nums, k) for i in (k + 1):length(nums) if !any(num1 + num2 == nums[i] for (num1, num2) in combinations(nums[i-k:i-1], 2)) return (i, nums[i]) end endend
function rectify(nums, k) v = bad_number(nums, k) i = j = 1 while (s = sum(nums[i:j])) != v s < v ? j += 1 : i += 1 end return minimum(nums[i:j]) + maximum(nums[i:j])end
input = readInput()part1 = bad_number(input, 25)part2 = rectify(input, 25)Day 10: Adapter Array
Part 2 on this day asks to find the number of distinct ways to arrange the Jolt adapters to connect the charging outlet to the device.
This problem can be formulated as a dynamic programming problem. This is most straightforward to solve using recursion and memoization. Here's Tom Kwong's solution:
function readInput() data = parse.(Int, split(strip(read(joinpath(@__DIR__, "./input.txt"), String)), '\n')) |> sort vcat(0, data, data[end]+3)end
part1(data = readInput()) = count(==(1), diff(data)) * count(==(3), diff(data))
function part2(data = readInput()) len = length(data) dct = Dict{Int,Int}() function helper(v, i) haskey(dct, i) && return dct[i] i == len && return 1 n1 = v[i+1] - v[i] <= 3 ? helper(v, i+1) : 0 n2 = i+2 <= len && v[i+2] - v[i] <= 3 ? helper(v, i+2) : 0 n3 = i+3 <= len && v[i+3] - v[i] <= 3 ? helper(v, i+3) : 0 val = n1 + n2 + n3 dct[i] = val return val end helper(data, 1)endOne key insight here is that the data doesn't contain jolt adapters that are only 1 or 3 apart.
julia> StatsBase.countmap(diff(readInput()))Dict{Int64, Int64} with 2 entries: 3 => 32 1 => 71Since any adapter that is 3 away can't be removed, the number of distinct ways is just the product of all the different ways you can choose two adapters from the set of 1 away adapters that are in between the 3 away adapters. Here's a solution based on Jonnie Diegelman's that takes advantage of that:
function readInput() data = parse.(Int, split(strip(read(joinpath(@__DIR__, "./input.txt"), String)), '\n')) |> sort data = vcat(0, data, data[end]+3) join(string.(diff(data)))end
part1(data = readInput()) = count(==('1'), data) * count(==('3'), data)part2(data = readInput()) = prod(binomial.(length.(split(data, '3', keepempty=false)), 2) .+ 1)This only works however when the set of 1 away adapters is not longer than 5 elements, which is the case in our puzzle inputs.
Alternatively, because the steps needed are one, two or three, you can calculate all possible steps
by using a tribonacci sum. The tribonacci sum gives us all ways to traverse a set of ones, i.e.
11111... by hopping from 1 to 1 in steps of size 1, 2 or 3.
Thanks to Sukera and Andrey Oskin for their code and insight into solving this puzzle.
function readInput() data = parse.(Int, split(strip(read(joinpath(@__DIR__, "./input.txt"), String)), '\n')) |> sort data = vcat(0, data, data[end]+3) split(join(string.(diff(data))), '3', keepempty = false)end
function tribonacci(n) n <= 1 && return 1 n == 2 && return 2 tribonacci(n-1) + tribonacci(n-2) + tribonacci(n-3)end
part2(data = readInput()) = prod(tribonacci.(length.(data)))The tribonacci sequence can also be generalized:
const a1 = (19 + 3sqrt(33))^(1/3)const a2 = (19 - 3sqrt(33))^(1/3)const b = (586 + 102sqrt(33))^(1/3)tribonacci(n) = round(Int, (3b * (1/3 * (a1 + a2 + 1))^(n + 1))/(b^2 - 2b + 4))See the Wikipedia article for more information.
Day 11: Seating System
This is the first tribute in Advent of Code 2020 to John Conway, who passed away earlier this year. John Conway was an English mathematician, most notably famous for the invention of the cellular automation called the Game of Life.
readInput() = permutedims(reduce(hcat, collect.(split(strip(read(joinpath(@__DIR__, "./input.txt"), String)), '\n'))))
part1(data = readInput()) = simulate(data, 0, 1)part2(data = readInput()) = simulate(data, 1, size(data, 1) * 2)
function simulate(grid, company, sight) while true old_grid = deepcopy(grid) tick(grid, company, sight) grid == old_grid && break end count(==('#'), grid)end
function tick(grid, company, sight) rows, cols = size(grid) old_grid = deepcopy(grid) for r in 1:rows, c in 1:cols A = adjacent_seats(old_grid, r, c, sight) grid[r, c] == 'L' && count(==('#'), A) == 0 && ( grid[r, c] = '#' ) grid[r, c] == '#' && count(==('#'), A) >= 4 + company && ( grid[r, c] = 'L' ) endend
function adjacent_seats(grid, i, j, sight) A = [] for direction in CartesianIndex.([(-1,-1), (-1,+1), (+1,-1), (+1, +1), (-1,0), (+1,0), (0,-1), (0,+1)]) xy = CartesianIndex(i, j) + direction counter = 1 while checkbounds(Bool, grid, xy) && grid[xy] == '.' && counter < sight xy += direction counter += 1 end checkbounds(Bool, grid, xy) && push!(A, grid[xy]) end AendThe key thing to remember when implementing cellular automata is to copy the grid at each tick.
Julia's CartesianIndex makes it easier to deal with multi-dimensional indexing. Additionally, I
found the checkbounds function quite handy for this problem.
Day 12: Rain Risk
This was one of my better performances on the Julia leaderboard. Using complex numbers makes it quite straightforward to deal with problems involving rotation.
readInput() = split(strip(read(joinpath(@__DIR__, "./input.txt"), String)), '\n')
function part1(data = readInput()) data = map(data) do d first(d), parse(Int, d[begin+1:end]) end current = 0 + 0im direction = 1 + 0im for (action, move) in data if action == 'N' current += move * im elseif action == 'S' current -= move * im elseif action == 'E' current += move elseif action == 'W' current -= move elseif action == 'F' current += direction * move elseif action == 'L' direction *= im^(move ÷ 90) elseif action == 'R' direction *= (-im)^(move ÷ 90) else error("Unrecognized $action, $move") end end abs(current.re) + abs(current.im)end
function part2(data = readInput()) data = map(data) do d first(d), parse(Int, d[begin+1:end]) end waypoint = 10 + 1im current = 0 + 0im direction = 1 + 0im for (action, move) in data if action == 'N' waypoint += move * im elseif action == 'S' waypoint -= move * im elseif action == 'E' waypoint += move elseif action == 'W' waypoint -= move elseif action == 'F' current += waypoint * move elseif action == 'L' waypoint *= im^(move ÷ 90) elseif action == 'R' waypoint *= (-im)^(move ÷ 90) else error("Unrecognized $action, $move") end end abs(current.re) + abs(current.im)endThanks to
Colin Caine
for suggesting using if ... elseif ... end for minor performance improvements. Check out his other
solutions for more optimized takes on the problems.
Michael Krabbe Borregaard had some neat visualizations for this day.
Day 13: Shuttle Search
This was one of the harder days for me. I had never heard of Chinese Remainder Theorem (CRT) and apparently that's what this problem was based on.
Here's a solution by
Micah Halter
that uses the CRT function from Mods.jl package.
using Mods
function readInput() t_str, buses_str = readlines(joinpath(@__DIR__, "./input.txt")) time = parse(Int, t_str) buses = map(x->x=="x" ? nothing : parse(Int, x), split(buses_str, ',')) time, busesend
function part1(data = readInput()) time, buses = data wait, bus = min(map(x->(x*ceil(time / x), x), filter(!isnothing, buses))...) (wait - time) * busend
function part2(data = readInput()) _, buses = data mods = map(k->Mod{buses[k]}(-(k-1)), filter(k->!isnothing(buses[k]), keys(buses))) CRT(mods...).valendHere's another solution from
Doug
that finds the cycles using lcm much more elegantly than how I ended up doing it. The key bit of
insight here is that the lcm(previous_bus_schedules, new_bus_schedule) will be the cycle at which
the pattern repeats. Using this, you can break the problem down by iteratively and calculate the
next cycle.
function readInput() input = readlines(joinpath(@__DIR__, "./input.txt")) n = parse(Int, input[1]) schedule = parse.(Int, replace(split(input[2], ","), "x" => "-1")) bus_n = filter(!=(-1), schedule) bus_dt = (1:length(schedule))[schedule .!= -1] .- 1 bus_n, bus_dt, nend
function part1(data = readInput()) bus_n, bus_dt, n = data min_rem, min_rem_i = findmin(bus_n .- n .% bus_n) bus_n[min_rem_i] * min_remend
function part2(data = readInput()) bus_n, bus_dt, n = data inc = bus_n[1] n = 0 for (i, offset) in zip(bus_n[2:end], bus_dt[2:end]) while (n + offset) % i != 0 n += inc end inc = lcm(inc, i) end return nendDay 14: Docking Data
This puzzle requires dealing with bit shifting and masking of bits.
Here's Pablo Zubieta's solution:
function parse_mask_ops(line) mask, list = split(line, r"\n"; limit = 2, keepempty = false) instructions = Tuple{Int,Int}[] for m in eachmatch(r"mem.(\d+). = (\d+)", list) address, n = m.captures push!(instructions, (parse(Int, address), parse(Int, n))) end return mask, instructionsend
readInput() = parse_mask_ops.(split(read(joinpath(@__DIR__, "./input.txt"), String), r"mask = "; keepempty = false))
struct Part1 endstruct Part2 end
function write!(::Part1, memory, mask, addr, n) for (i, bit) in enumerate(mask) if bit != 'X' m = 1 << (36 - i) n = (bit == '1') ? (n | m) : (n & ~m) end end memory[addr] = nend
function write!(::Part2, memory, mask, addr, n) inds = Int8[] for (i, bit) in enumerate(mask) if bit == '1' addr |= (1 << (36 - i)) elseif bit == 'X' push!(inds, i) end end l = length(inds) for p in 0:(2^l - 1) for (k, i) in enumerate(inds) m = 1 << (36 - i) b = (p >> (l - k)) & 1 addr = b != 0 ? (addr | m) : (addr & ~m) end memory[addr] = n endend
function solve(p::Union{Part1,Part2}, input) memory = Dict{Int,Int}() for (mask, list) in input for (address, n) in list write!(p, memory, mask, address, n) end end return sum(values(memory))end
part1(data = readInput()) = solve(Part1(), data)part2(data = readInput()) = solve(Part2(), data)I liked this solution because it was clean and fast:
julia> @btime part1(); 392.104 μs (2987 allocations: 251.47 KiB)
julia> @btime part2(); 5.218 ms (4426 allocations: 5.96 MiB)For comparison, these were the times from my original solution:
julia> @btime part1(); 2.860 ms (75635 allocations: 4.77 MiB)
julia> @btime part2(); 287.836 ms (6234948 allocations: 319.65 MiB)There are more optimized solutions though, for example here are the timings for the solution posted by Colin Caine:
julia> @btime part1(); 25.614 μs (14 allocations: 23.98 KiB)
julia> @btime part2(); 3.354 ms (41 allocations: 5.67 MiB)
julia> @btime part2a(); 2.865 ms (37 allocations: 5.67 MiB)Day 15: Rambunctious Recitation
This puzzle seemed to mainly focus on choosing the right data structure for the history of the
memory game. Storing it as a mapping of number to list of indices works well for both parts. A
mapping of indices to number will cause the code to be slow, and will make solving part 2
impractical.
Here's a solution by Sukera:
readInput() = parse.(Int, split(readline(joinpath(@__DIR__, "./input.txt")), ','))
makeArr() = Int[]
function solve(input, goal=2020) history = Dict{Int, Vector{Int}}() for (idx, num) in enumerate(input) history[num] = [idx] end turn = length(input) + 1 num = 0 for t in turn:goal-1 arr = get!(history, num, makeArr()) push!(arr, t) if isone(length(arr)) num = 0 else num = abs(arr[end-1] - arr[end]) end end numend
part1(data = readInput()) = solve(data)part2(data = readInput()) = solve(data, 30000000)This video is worth checking out too:
Day 16: Ticket Translation
Calculating which fields were invalid for part 1 was rather straightforward.
function readInput() data = strip(read(joinpath(@__DIR__, "./input.txt"), String)) rules, your_ticket, nearby_tickets = split(data, "\n\n") rules = Dict(map(split(rules, '\n')) do rule rule, r1start, r1end, r2start, r2end = match(r"([\w ]+): (\d+)-(\d+) or (\d+)-(\d+)", rule) r1start, r1end, r2start, r2end = parse.(Int, [r1start, r1end, r2start, r2end]) rule => (r1start:r1end, r2start:r2end) end) your_ticket = parse.(Int, split(split(your_ticket, '\n')[2], ',')) nearby_tickets = [parse.(Int, ticket) for ticket in split.(split(nearby_tickets, '\n')[2:end], ',')] rules, your_ticket, nearby_ticketsend
function part1(data = readInput()) rules, your_ticket, nearby_tickets = data invalid_fields = Int[] for ticket in nearby_tickets, field in ticket !any([field ∈ rule for rule in Iterators.flatten(values(rules))]) && push!(invalid_fields, field) end sum(invalid_fields)endI believe part 2 is better expressed as a graph where you solve the max flow problem to find the maximum matching. However, this is not how I solved it below. I'm hoping to re-solve this problem using LightGraphs.jl.
function part2(data = readInput()) rules, your_ticket, nearby_tickets = data
invalid_tickets = Int[] for (i, ticket) in enumerate(nearby_tickets), field in ticket !any([field ∈ rule for rule in Iterators.flatten(values(rules))]) && push!(invalid_tickets, i) end valid_tickets = deleteat!(nearby_tickets, invalid_tickets)
valid = ones(Bool, length(first(valid_tickets)), length(rules)) for ticket in valid_tickets, (i, field) in enumerate(ticket), (j, rule) in enumerate(rules) _, (rule1, rule2) = rule !(field ∈ rule1 || field ∈ rule2) && ( valid[i, j] = false ) end
final = [0 for _ in 1:length(rules)] accounted_for = Set{Int}() while length(accounted_for) != length(rules) for i in 1:length(first(valid_tickets)) valid_rules = [j for j in 1:length(rules) if valid[i, j] && j ∉ accounted_for] if length(valid_rules) == 1 final[i] = only(valid_rules) push!(accounted_for, only(valid_rules)) end end end
answer = 1 for (interest, k) in enumerate(keys(rules)) !startswith(k, "departure") && continue for (i, index) in enumerate(final) index == interest && ( answer *= your_ticket[i] ) end end answerendMy learning from this day was that in Julia you can refactor the code with multiple nested for
loops:
for ticket in valid_tickets for (i, field) in enumerate(ticket) for (j, rule) in enumerate(rules) _, (rule1, rule2) = rule !(field ∈ rule1 || field ∈ rule2) && ( valid[i, j] = false ) end endendinto a single line like so:
for ticket in valid_tickets, (i, field) in enumerate(ticket), (j, rule) in enumerate(rules) _, (rule1, rule2) = rule !(field ∈ rule1 || field ∈ rule2) && ( valid[i, j] = false )endYou can even use the variable from the outer loop as the index in the inner loop, like you'd expect. This can help reduce the nesting level of your inner expressions.
Day 17: Conway Cubes
Another homage to John Conway, this time in multiple dimensions.
Here's Michael Krabbe Borregaard's succinct solution that takes
advantage of CartesianIndices:
function parsefield(lines, n, dims) field = falses(fill(n, dims)...) for (i,line) in enumerate(lines), (j, char) in enumerate(line) char == '#' && (field[i + n÷2, j + n÷2, fill(n÷2, dims-2)...] = true) end fieldend
function startup(lines, rounds, dims) field = parsefield(lines, 2*(length(lines) + rounds + 2), dims) newfield = copy(field) for n in 1:rounds for ind in CartesianIndices(field)[fill(2+rounds-n:size(field, 1)-rounds-1+n, dims)...] counter = sum(field[((-1:1) .+ i for i in Tuple(ind))...]) - field[ind] newfield[ind] = field[ind] ? counter in (2,3) : counter == 3 end field .= newfield end sum(field)end
readInput() = readlines(joinpath(@__DIR__, "./input.txt"))part1(data = readInput()) = startup(data, 6, 3)part2(data = readInput()) = startup(data, 6, 4)Cellular automata puzzles are always fun, and make for some neat visualizations. Here are a couple of multi dimensional visualizations by Tom Kwong:


Day 18: Operation Order
The intended way to solve such problems is by implementing the Shunting-yard algorithm.
However, you can hack the operator precedence in your programming language of choice and take advantage of the built in parser.
Here is Doug's that managed to get him a spot on the global leaderboard.
readInput() = readlines(joinpath(@__DIR__, "./input.txt"))
⨦(a,b) = a * b # define "multiplication" with same precedence as "+"part1(data = readInput()) = sum(l -> eval(Meta.parse(replace(l, "*" => "⨦"))), data)
⨱(a,b) = a + b # define "addition" with precedence of "*"part2(data = readInput()) = sum(l -> eval(Meta.parse(replace(replace(l, "*" => "⨦"), "+" => "⨱"))), data)The key is to find the right operators in your programming language that have the precedence required as per the prompt.
Day 19: Monster Messages
This was another hard day for me. First, I tried to implement a recursive algorithm. After failing to figure this out, I picked it up again on the next day with a clean slate, and I tried to build a regex that would match various messages. This worked for part 1 but I kept running out of memory for part 2. Finally, after changing some of the rules hard-coding them by hand I was able to solve part 2.
Specifically, I hard coded rules "8" and "11" to the following.
rules["8"] = "(42)+"rules["11"] = "42 31 | 42 ( 42 31 | 42 ( 42 31 | 42 ( 42 31 | 42 ( 42 31 ) 31 ) 31 ) 31 ) 31"This limits the depth of rule "11". One more step however and I was getting PCRE memory errors.
Here's a solution by Doug that does the same thing elegantly and programmatically.
function readInput() rules, messages = split.(split(strip(read(joinpath(@__DIR__, "./input.txt"), String)), "\n\n"), '\n') rules = Dict(map(rules) do line m = match(r"^(\d+): (\"(\w+)\"|([^|]+)|(.+))$", line) String(m[1]) => m[3] isa Nothing ? (m[4] isa Nothing ? "(?:$(m[5]))" : String(m[4])) : String(m[3]) end) rules, messagesend
function resolve(rule, rules) ns = [nsi.match for nsi = eachmatch(r"\b\d+\b", rule)] n_res = [Regex("\\b$nsi\\b") for nsi = ns] n_rep = [resolve(rules[nsi], rules) for nsi=ns] replace(reduce(replace, n_res .=> n_rep, init = rule), " " => "")end
function part1(data = readInput()) rules, messages = data count(contains(Regex("^$(resolve(rules["0"], rules))\$")), messages)end
function part2(data = readInput()) rules, messages = data rule42 = resolve(rules["42"], rules) rule31 = resolve(rules["31"], rules) count(contains(Regex("^$rule42+($rule42(?1)?$rule31)\$")), messages)endAs noted by /u/furiousleep on /r/adventofcode (along with other valuable feedback), the intended solution for this would use the CYK algorithm. I would like to rewrite my solution using this algorithm instead.
Day 20: Jurassic Jigsaw
This puzzle was really fun to figure out but also tedious to type out everything that you needed to type out. While I was able to solve the problem, I hard-coded many things in my solution. My code doesn't even work for the test cases. This is just one of those puzzles that is easier to solve on paper than to write an actual working implementation.
Here's a working solution by Alisdair Sullivan:
readInput() = map(t -> split(t, "\n"), split(strip(read(joinpath(@__DIR__, "./input.txt"), String)), "\n\n"))
mutable struct Tile id::Int raw::Array{Char, 2}end
function copy(tile::Tile) new = copy(tile.raw) return Tile(tile.id, new)end
t = Tile(1, ['a' 'b' 'c'; 'd' 'e' 'f'])
function size(tile::Tile) return Base.size(tile.raw)end
function top(tile::Tile) (y, x) = size(tile) return tile.raw[range(1, length=x, step=y)]end
function right(tile::Tile) (y, x) = size(tile) return tile.raw[range((x * y) - y + 1, length=y, step=1)]end
function bottom(tile::Tile) (y, x) = size(tile) return tile.raw[range(y, length=x, step=y)]end
function left(tile::Tile) (y, x) = size(tile) return tile.raw[range(1, length=y, step=1)]end
function flip!(tile) new = tile.raw[:,end:-1:1] tile.raw = newend
function rotate!(tile) new = rotr90(tile.raw) tile.raw = newend
function parse_tiles(tiles) return map(tile -> parse_tile(tile), tiles)end
function parse_tile(tile) m = match(r"(\d+)", first(tile)) id = parse(Int, m.captures[1]) raw = reduce(vcat, permutedims.(collect.(tile[2:end]))) return Tile(id, raw)end
function find_edges(tile) edges = [] push!(edges, top(tile)) push!(edges, right(tile)) push!(edges, bottom(tile)) push!(edges, left(tile)) push!(edges, reverse(top(tile))) push!(edges, reverse(right(tile))) push!(edges, reverse(bottom(tile))) push!(edges, reverse(left(tile))) return edgesend
function orient!(tile, matches) for flipped in (false, true), i in 1:4 matches(tile) && return flipped && flip!(tile) flipped && matches(tile) && return flipped && flip!(tile) rotate!(tile) endend
function find_corners(tiles) corners = [] ec = count_edges(tiles)
for tile in tiles c = sum([length(ec[top(tile)]), length(ec[bottom(tile)]), length(ec[left(tile)]), length(ec[right(tile)])]) c == 6 && push!(corners, tile) end return cornersend
function count_edges(tiles) acc = Dict{Vector{Char}, Vector{Int}}() for tile in tiles edges = find_edges(tile) for edge in edges haskey(acc, edge) ? acc[edge] = append!(acc[edge], tile.id) : acc[edge] = [tile.id] end end return accend
function find_origin(tiles) edges = count_edges(tiles) corner = first(find_corners(tiles)) for _ in 1:4 t = edges[top(corner)] l = edges[left(corner)] length(t) == 1 && length(l) == 1 && return corner rotate!(corner) endend
function trim(tile) raw = tile.raw (x, y) = size(tile) return raw[2:(x - 1),2:(y - 1)]end
function assemble(tiles) origin = find_origin(deepcopy(tiles)) edges = count_edges(deepcopy(tiles))
rows = [] row = [origin]
rowstart = origin current = origin
while !isnothing(current) match = edges[right(current)] if length(match) == 2 next_id = only(filter(id -> id != current.id, match)) next_idx = findfirst(t -> t.id == next_id, tiles) next = tiles[next_idx] matcher = (t) -> left(t) == right(current) orient!(next, matcher) push!(row, next) current = next else push!(rows, row) match = edges[bottom(rowstart)] if length(match) == 2 next_id = only(filter(id -> id != rowstart.id, match)) next_idx = findfirst(t -> t.id == next_id, tiles) next = tiles[next_idx] orient!(next, (t) -> top(t) == bottom(rowstart)) current = next rowstart = current row = [rowstart] else current = nothing end end end
return vcat(map(row -> hcat(map(tile -> trim(tile), row)...), rows)...)end
function find_seamonsters(assembled) # seamonster pattern indices = [ CartesianIndex(19, 1), CartesianIndex(1, 2), CartesianIndex(6, 2), CartesianIndex(7, 2), CartesianIndex(12, 2), CartesianIndex(13, 2), CartesianIndex(18, 2), CartesianIndex(19, 2), CartesianIndex(20, 2), CartesianIndex(2, 3), CartesianIndex(5, 3), CartesianIndex(8, 3), CartesianIndex(11, 3), CartesianIndex(14, 3), CartesianIndex(17, 3) ]
(xr, yr) = Base.size(assembled) .- (20, 3)
counts = []
for flipped in (false, true), i in 1:4 flipped ? assembled = assembled[end:-1:1,:] : nothing count = 0 idx = CartesianIndex(0,0) for j in 1:yr (x, y) = Tuple(idx) idx = CartesianIndex(0, y + 1) for i in 1:xr idx += CartesianIndex(1, 0) all(i -> assembled[idx + i] == '#', indices) ? count += 1 : nothing end end push!(counts, count) flipped ? assembled = assembled[end:-1:1,:] : nothing assembled = rotr90(assembled) end return countsend
function check(puzzle) acc = 0 for i in eachindex(puzzle) puzzle[i] == '#' ? acc += 1 : nothing end return accend
function part1(tiles = readInput()) tiles = parse_tiles(tiles) corners = find_corners(tiles) prod(map(tile -> tile.id, corners))end
function part2(tiles = readInput()) tiles = parse_tiles(tiles) corners = find_corners(tiles)
assembled = assemble(tiles) counts = find_seamonsters(assembled)
check(assembled) - (maximum(counts) * 15)endThe key functions I found that others were using were rotl90, rotr90 and rot180 from the Julia
standard library, like in
Pablo Zubieta's solution.
Mark Kittisopikul
also used imfilter from ImageFiltering.jl to
find the monsters, which I thought was pretty neat.
Day 21: Allergen Assessment
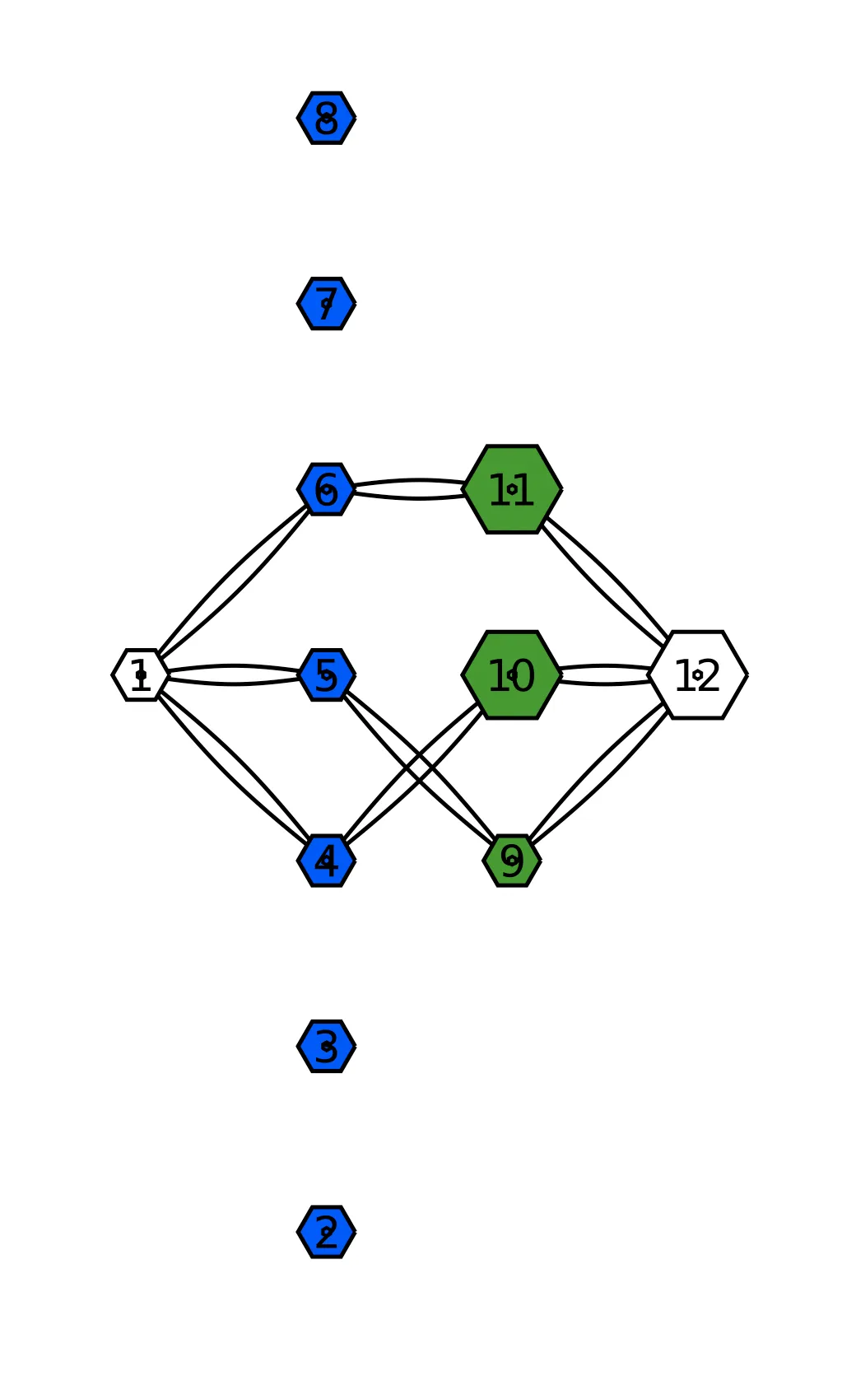
This puzzle is another graph problem that can be solved quite elegantly using maximum flow algorithms to find the maximum matching. Here's the solution of the test case using LightGraphs.jl and LightGraphFlows.jl, as well as a visualization using GraphRecipes.jl and Plots.jl:
using LightGraphsusing LightGraphsFlowsusing GraphRecipes, Plots
readInput() = strip(read(joinpath(@__DIR__, "./input.txt"), String))
function m() data = split(strip(readInput()), '\n') data = map(data) do line ingredients, allergens = match(r"^(.*) \(contains (.*)\)$", line).captures String.(split(ingredients)), String.(split(allergens, ", ")) end
all_ingredients, all_allergens = Set{String}(), Set{String}() for (ingredients, allergens) in data all_ingredients = all_ingredients ∪ Set(ingredients) all_allergens = all_allergens ∪ Set(allergens) end all_ingredients, all_allergens = collect(all_ingredients), collect(all_allergens)
d = Dict() for (ingredients, allergens) in data, allergen in allergens allergen ∉ keys(d) && ( d[allergen] = Set(ingredients) ) d[allergen] = d[allergen] ∩ Set(ingredients) end
MAX_NODES = length(all_ingredients) + length(all_allergens) + 2 g = SimpleDiGraph(MAX_NODES) for i in all_ingredients i = 1 + findfirst(==(i), all_ingredients) add_edge!(g, 1, i) end for a in all_allergens a = length(all_ingredients) + 1 + findfirst(==(a), all_allergens) add_edge!(g, a, MAX_NODES) end for (allergen, ingredients) in d, ingredient in ingredients i = 1 + findfirst(==(ingredient), all_ingredients) a = 1 + length(all_ingredients) + findfirst(==(allergen), all_allergens) add_edge!(g, i, a) end
graphplot(g, names = 1:MAX_NODES, x = vcat([[1]; [2 for _ in 1:length(all_ingredients)]; [3 for _ in 1:length(all_allergens)]; [4]]), y = vcat( [ [1]; [i - length(all_ingredients) ÷ 2 for i in 1:length(all_ingredients)]; [a - length(all_allergens) ÷ 2 for a in 1:length(all_allergens)]; [1] ] ), markercolor = vcat([ [colorant"white"]; [colorant"blue" for _ in 1:length(all_ingredients)]; [colorant"green" for _ in 1:length(all_allergens)]; [colorant"white"] ]), markersize = 1)
_, F = maximum_flow(g, 1, MAX_NODES)
no_allergen_ingredients = all_ingredients[[i - 1 for i in 1:MAX_NODES if count(==(0), F[i, :]) == MAX_NODES]]
no_allergen_ingredients sum(map(data) do (ingredients, _) count(i ∈ ingredients for i in no_allergen_ingredients) end)endHere are a couple of visualizations, the test data visualized as a graph is on the left and the maximum flow solution on the right.
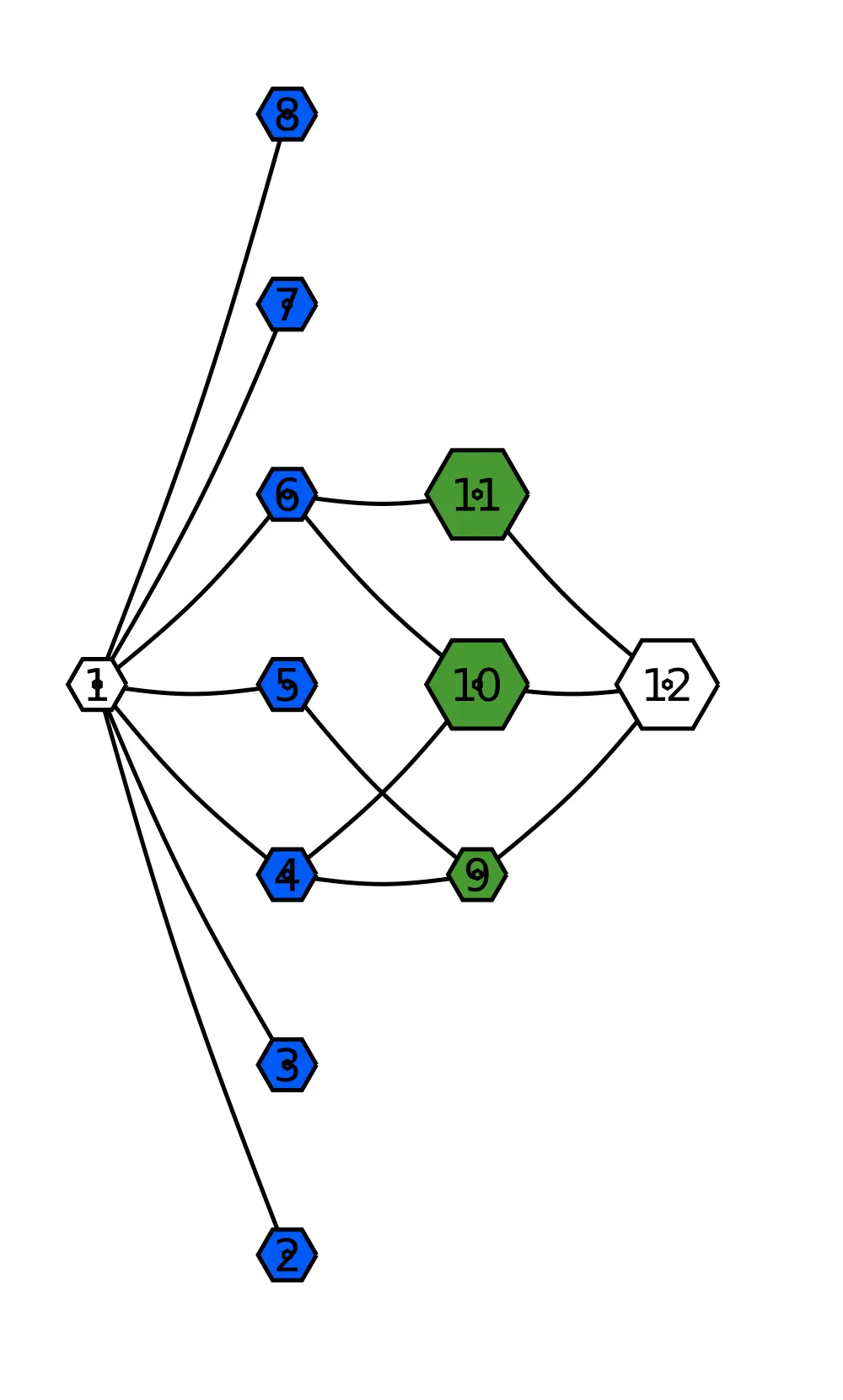
Day 22: Crab Combat
This puzzle was mostly straightforward too. The key here seems to be to implement the stopping conditions correctly, and take advantage of the stack based behavior of recursion in most programming languages.
Here's a solution by Henrique Ferrolho's.
function play(p₁, p₂, part₂) seen = Set{Tuple{Array,Array}}([])
while !any(isempty.((p₁, p₂))) (p₁, p₂) ∈ seen && return 1, p₁ # infinite-game-prevention rule push!(seen, copy.((p₁, p₂)))
c₁, c₂ = popfirst!.((p₁, p₂)) # both players draw their top card
if part₂ && all(length.((p₁, p₂)) .>= (c₁, c₂)) w, _ = play(copy.((p₁[1:c₁], p₂[1:c₂]))..., part₂) elseif c₁ > c₂ w = 1 elseif c₂ > c₁ w = 2 else @error "Unexpected case: c₁ == c₂" end
w == 1 && push!(p₁, c₁, c₂) # player 1 wins w == 2 && push!(p₂, c₂, c₁) # player 2 wins end
!isempty(p₁) ? (1, p₁) : (2, p₂)end
function day22() p₁, p₂ = split(read(joinpath(@__DIR__, "./input.txt"), String), "\n\n") .|> x -> parse.(Int, split(x, '\n', keepempty=false)[2:end])
result₁, result₂ = map([false, true]) do part₂ _, deck = play(copy.((p₁, p₂))..., part₂) multipliers = length(deck):-1:1 sum(deck .* multipliers) end
result₁, result₂end
part1() = day22()[1]part2() = day22()[2]Julia allows using unicode symbols as part of variable names which can make for some pretty looking code.
Day 23: Crab Cups
This puzzle took me a while to figure out. I spent way too long looking for patterns in each state. Thanks to some helpful tips from fellow Julia advent-of-coders, I re-wrote it from scratch using a Linked List.
The key idea is here to manage the ordering in a separate data structure. Using a linked list is just one way to handle this.
Here's a solution by Nicolas Viennot based on exchanging ideas with Teo ShaoWei that manages to do that quite elegantly using another array to manage indices:
readInput() = parse.(Int32, collect(strip(read(joinpath(@__DIR__, "./input.txt"), String))))
function peek(next, at, n; result=similar(next,n)) for i in 1:n result[i] = next[at] at = next[at] end resultend
function run(cups, steps=1) N = length(cups) prealloc = similar(cups, 3)
next = similar(cups) for i in 1:N next[cups[i]] = cups[mod1(i+1,N)] end
current = cups[1] for i in 1:steps pickups = peek(next, current, 3, result=prealloc)
dst = mod1(current-1, N) while dst in pickups dst = mod1(dst-1, N) end
next[current] = next[pickups[end]] next[pickups[end]] = next[dst] next[dst] = pickups[1] current = next[current] end
return nextend
part1(cups = readInput()) = join(peek(run(cups, 100), 1, 8))part2(cups = readInput()) = prod(peek(run(vcat(cups, 10:1_000_000), 10_000_000), 1, 2))Day 24: Lobby Layout
In another tribute to John Conway, now you must model hexagon grids.
Having never worked with hexagon grid before, I reached for complex numbers again, which turned out to be a bad idea. I was indexing a dictionary with the real and imaginary components of the complex number which were floating point numbers. This caused all sorts of indexing problems due to rounding issues.
I could have sorted this out by using only integer values or by using the coordinate system described in this resource: https://www.redblobgames.com/grids/hexagons/#coordinates-cube.
Here's another elegant solution by Nicolas Viennot.
using OffsetArrays
parse_path(line) = getproperty.(eachmatch(r"(e|se|sw|w|nw|ne)", line), :match)readInput() = parse_path.(readlines(joinpath(@__DIR__, "./input.txt")))
const hex_dirs = Dict(k => CartesianIndex(v) for (k,v) in [ "e" => ( 1, 0), "se" => ( 1, -1), "sw" => ( 0, -1), "w" => (-1, 0), "nw" => (-1, 1), "ne" => ( 0, 1)])
const N = 200
get_destination(path) = mapreduce(x->hex_dirs[x], +, path)
function init_tiles(paths) A = OffsetArray(falses(N,N),-N÷2-1,-N÷2-1) foreach(dst -> A[dst] ⊻= 1, get_destination.(paths)) Aend
part1(data = readInput()) = count(init_tiles(data))
function get_neighbor_counts(A) C = OffsetArray(zeros(Int, N-2,N-2),-N÷2,-N÷2) for i in CartesianIndices(C) C[i] = sum(A[i+dir] for dir in values(hex_dirs)) end Cend
function flip_tiles!(A, steps=1) for step in 1:steps C = get_neighbor_counts(A) for i in CartesianIndices(C) if (A[i] && C[i] ∉ (1,2)) || (!A[i] && C[i] == 2) A[i] ⊻= 1 end end end Aend
part2(data = readInput()) = count(flip_tiles!(init_tiles(data), 100))And another neat visualization by Tom Kwong:

Day 25: Combo Breaker
And finally, for the last day, it is a cryptography based puzzle.
The puzzle's key idea here is based on the Diffie-Hellman key exchange.
Julia also has a function called powermod in the standard library, which can be used for this.
Here's a solution by Nicolas Viennot:
readInput() = parse.(Int, split(strip(read(joinpath(@__DIR__, "./input.txt"), String)), '\n'))
function part1(data = readInput()) N = 20201227 e = 7 card_public_key, door_public_key = data privkey1 = findfirst(i -> powermod(e, i, N) == card_public_key, 1:N) solution = powermod(door_public_key, privkey1, N)endIf you've made it all this way, part 2 of day 25 should be a cinch 😉.
Final words
Thanks to everyone in the Julia community who participated on Zulip, Slack and Reddit. I learnt a lot by reading your solutions and discussing with you all.
Thanks to the mods on /r/adventofcode to making it such a vibrant community to frequent.
And finally, thanks to Eric Wastl for making such a fun event.
Happy holidays everyone!
Footnotes
-
aside: Python has a similar function in the standard library: https://docs.python.org/3/library/itertools.html#itertools.combinations ↩