Validation 08 - Timeseries Ramp Rates

%matplotlib inline

import psst

from psst.case import read_matpower
from psst.network import create_network
import pandas as pd

Validation of case 1

case = read_matpower('./cases/case7.m')

case.load = pd.read_csv('./cases/case7.csv', index_col=0)

network = create_network(case, prog='neato')
network.draw()

case

<psst.case.PSSTCase(name=casematpower, Generators=2, Buses=2, Branches=1)>

case.bus

	TYPE	PD	QD	GS	BS	AREA	VM	VA	BASEKV	ZONE	VMAX	VMIN
Bus1	3	0	131.47	0	0	1	1	0	230	1	1.1	0.9
Bus2	2	100	0.00	0	0	1	1	0	230	1	1.1	0.9

case.branch

	F_BUS	T_BUS	BR_R	BR_X	BR_B	RATE_A	RATE_B	RATE_C	TAP	SHIFT	BR_STATUS	ANGMIN	ANGMAX
0	Bus1	Bus2	0.00281	0.0281	0.00712	800	800	800	0	0	1	-360	360

case.gen.loc['GenCo1', 'RAMP_10'] = 50

case.gen

	GEN_BUS	PG	QG	QMAX	QMIN	VG	MBASE	GEN_STATUS	PMAX	PMIN	PC1	PC2	QC1MIN	QC1MAX	QC2MIN	QC2MAX	RAMP_AGC	RAMP_10	RAMP_30	RAMP_Q	APF	STARTUP_RAMP	SHUTDOWN_RAMP
GenCo0	Bus1	200	0	30	-30	1	100	1	200	0	0	0	0	0	0	0	0	200.0	0	0	0	200	200
GenCo1	Bus2	500	0	30	-30	1	100	1	500	0	0	0	0	0	0	0	0	50.0	0	0	0	500	500

case.gencost.loc['GenCo1', 'STARTUP'] = 0
case.gencost.loc['GenCo1', 'SHUTDOWN'] = 0

case.gencost

	MODEL	STARTUP	SHUTDOWN	NCOST	COST_1	COST_0
GenCo0	1	0	0	2	10	0
GenCo1	1	0	0	2	14	2000

import matplotlib.pyplot as plt

fig, axs = plt.subplots(1, 1, figsize=(8, 5))
ax = axs
case.load['Bus2'].plot.bar(ax=ax)
ax.set_ylim(0, 500);

from psst.model import build_model

model = build_model(case)

model

<psst.model.PSSTModel(status=None)>

model.solve(solver='cbc', verbose=True)

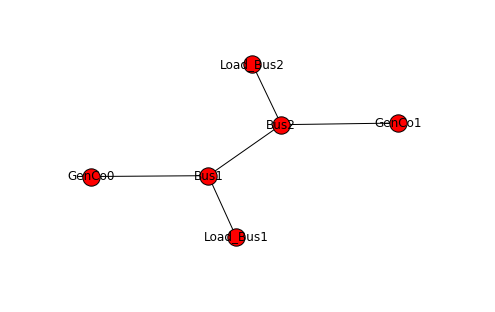
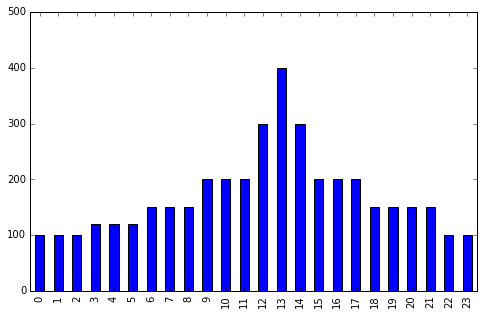
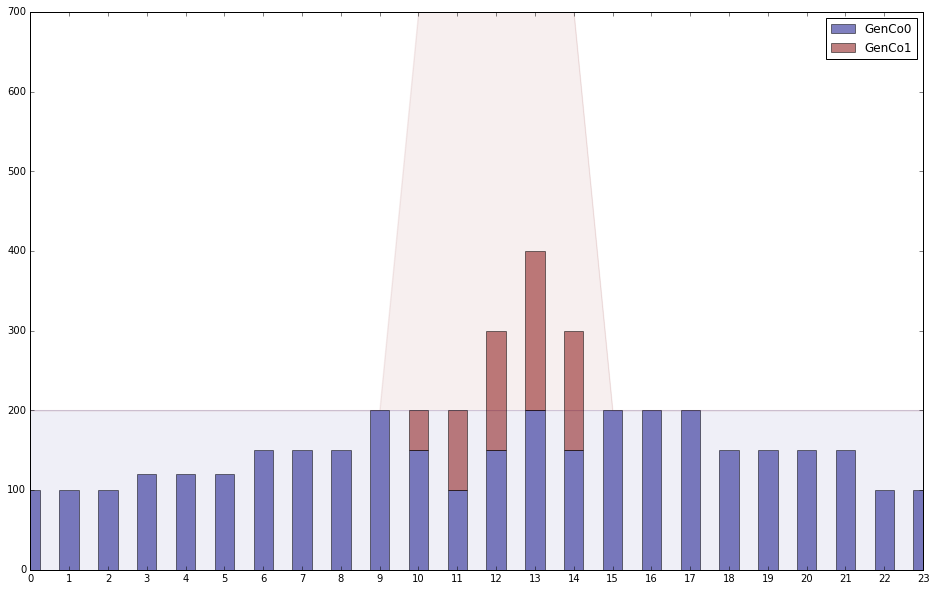
Welcome to the CBC MILP Solver
Version: 2.9.6
Build Date: May 27 2016

command line - /usr/local/bin/cbc -mipgap 0.01 -printingOptions all -import /var/folders/wk/lcf0vgd90bx0vq1873tn04knk_djr3/T/tmpQouRDK.pyomo.lp -import -stat=1 -solve -solu /var/folders/wk/lcf0vgd90bx0vq1873tn04knk_djr3/T/tmpQouRDK.pyomo.soln (default strategy 1)
No match for mipgap - ? for list of commands
No match for 0.01 - ? for list of commands
Option for printingOptions changed from normal to all
Current default (if $ as parameter) for import is /var/folders/wk/lcf0vgd90bx0vq1873tn04knk_djr3/T/tmpQouRDK.pyomo.lp
Presolve 262 (-637) rows, 336 (-417) columns and 855 (-1409) elements
Statistics for presolved model
Original problem has 48 integers (48 of which binary)
Presolved problem has 24 integers (24 of which binary)
==== 120 zero objective 4 different
120 variables have objective of 0
48 variables have objective of 1
24 variables have objective of 2000
144 variables have objective of 1e+06
==== absolute objective values 4 different
120 variables have objective of 0
48 variables have objective of 1
24 variables have objective of 2000
144 variables have objective of 1e+06
==== for integers 0 zero objective 1 different
24 variables have objective of 2000
==== for integers absolute objective values 1 different
24 variables have objective of 2000
===== end objective counts


Problem has 262 rows, 336 columns (216 with objective) and 855 elements
There are 192 singletons with objective
Column breakdown:
240 of type 0.0->inf, 48 of type 0.0->up, 0 of type lo->inf,
24 of type lo->up, 0 of type free, 0 of type fixed,
0 of type -inf->0.0, 0 of type -inf->up, 24 of type 0.0->1.0
Row breakdown:
24 of type E 0.0, 0 of type E 1.0, 0 of type E -1.0,
48 of type E other, 0 of type G 0.0, 0 of type G 1.0,
0 of type G other, 72 of type L 0.0, 0 of type L 1.0,
118 of type L other, 0 of type Range 0.0->1.0, 0 of type Range other,
0 of type Free
Continuous objective value is 44300 - 0.00 seconds
Cgl0003I 0 fixed, 0 tightened bounds, 47 strengthened rows, 0 substitutions
Cgl0003I 0 fixed, 0 tightened bounds, 1 strengthened rows, 0 substitutions
Cgl0003I 0 fixed, 0 tightened bounds, 1 strengthened rows, 0 substitutions
Cgl0003I 0 fixed, 0 tightened bounds, 1 strengthened rows, 0 substitutions
Cgl0003I 0 fixed, 0 tightened bounds, 1 strengthened rows, 0 substitutions
Cgl0003I 0 fixed, 0 tightened bounds, 1 strengthened rows, 0 substitutions
Cgl0003I 0 fixed, 0 tightened bounds, 1 strengthened rows, 0 substitutions
Cgl0003I 0 fixed, 0 tightened bounds, 1 strengthened rows, 0 substitutions
Cgl0003I 0 fixed, 0 tightened bounds, 1 strengthened rows, 0 substitutions
Cgl0004I processed model has 238 rows, 335 columns (24 integer (24 of which binary)) and 805 elements
Cbc0038I Initial state - 1 integers unsatisfied sum - 0.2
Cbc0038I Pass   1: suminf.    0.00000 (0) obj. 1.5005e+08 iterations 12
Cbc0038I Solution found of 1.5005e+08
Cbc0038I Relaxing continuous gives 1.5005e+08
Cbc0038I Before mini branch and bound, 23 integers at bound fixed and 215 continuous
Cbc0038I Full problem 238 rows 335 columns, reduced to 8 rows 9 columns
Cbc0038I Mini branch and bound improved solution from 1.5005e+08 to 1.5005e+08 (0.03 seconds)
Cbc0038I Round again with cutoff of 1.3505e+08
Cbc0038I Pass   2: suminf.    0.02000 (1) obj. 1.3505e+08 iterations 1
Cbc0038I Pass   3: suminf.    0.00000 (0) obj. 1.3505e+08 iterations 4
Cbc0038I Solution found of 1.3505e+08
Cbc0038I Relaxing continuous gives 53700
Cbc0038I Before mini branch and bound, 23 integers at bound fixed and 213 continuous
Cbc0038I Mini branch and bound did not improve solution (0.04 seconds)
Cbc0038I Round again with cutoff of 53340
Cbc0038I Reduced cost fixing fixed 13 variables on major pass 3
Cbc0038I Pass   4: suminf.    0.20000 (1) obj. 53340 iterations 0
Cbc0038I Pass   5: suminf.    0.09474 (1) obj. 53340 iterations 10
Cbc0038I Pass   6: suminf.    1.48000 (4) obj. 53340 iterations 10
Cbc0038I Pass   7: suminf.    0.60000 (2) obj. 53340 iterations 13
Cbc0038I Pass   8: suminf.    0.14222 (2) obj. 53340 iterations 12
Cbc0038I Pass   9: suminf.    0.14222 (2) obj. 53340 iterations 4
Cbc0038I Pass  10: suminf.    0.14222 (2) obj. 53340 iterations 1
Cbc0038I Pass  11: suminf.    0.85060 (5) obj. 53340 iterations 9
Cbc0038I Pass  12: suminf.    0.85060 (5) obj. 53340 iterations 0
Cbc0038I Pass  13: suminf.    0.14222 (2) obj. 53340 iterations 8
Cbc0038I Pass  14: suminf.    0.09474 (1) obj. 53340 iterations 3
Cbc0038I Pass  15: suminf.    0.20000 (1) obj. 53340 iterations 16
Cbc0038I Pass  16: suminf.    1.48000 (4) obj. 53340 iterations 16
Cbc0038I Pass  17: suminf.    0.60000 (2) obj. 53340 iterations 12
Cbc0038I Pass  18: suminf.    0.14222 (2) obj. 53340 iterations 11
Cbc0038I Pass  19: suminf.    0.48000 (2) obj. 53340 iterations 2
Cbc0038I Pass  20: suminf.    0.57000 (3) obj. 53340 iterations 9
Cbc0038I Pass  21: suminf.    0.14222 (2) obj. 53340 iterations 12
Cbc0038I Pass  22: suminf.    0.09474 (1) obj. 53340 iterations 6
Cbc0038I Pass  23: suminf.    0.20000 (1) obj. 53340 iterations 17
Cbc0038I Pass  24: suminf.    0.84013 (6) obj. 53340 iterations 12
Cbc0038I Pass  25: suminf.    0.48000 (2) obj. 53340 iterations 8
Cbc0038I Pass  26: suminf.    0.48000 (2) obj. 53340 iterations 2
Cbc0038I Pass  27: suminf.    1.21810 (6) obj. 53340 iterations 3
Cbc0038I Pass  28: suminf.    0.47100 (5) obj. 53340 iterations 6
Cbc0038I Pass  29: suminf.    0.67610 (5) obj. 53340 iterations 3
Cbc0038I Pass  30: suminf.    0.47100 (5) obj. 53340 iterations 2
Cbc0038I Pass  31: suminf.    0.67610 (5) obj. 53340 iterations 1
Cbc0038I Pass  32: suminf.    1.31990 (7) obj. 53340 iterations 4
Cbc0038I Pass  33: suminf.    1.19999 (6) obj. 53340 iterations 5
Cbc0038I No solution found this major pass
Cbc0038I Before mini branch and bound, 14 integers at bound fixed and 199 continuous
Cbc0038I Full problem 238 rows 335 columns, reduced to 53 rows 40 columns
Cbc0038I Mini branch and bound improved solution from 53700 to 53700 (0.06 seconds)
Cbc0038I Round again with cutoff of 52908
Cbc0038I Reduced cost fixing fixed 13 variables on major pass 4
Cbc0038I Pass  33: suminf.    0.20000 (1) obj. 52908 iterations 0
Cbc0038I Pass  34: suminf.    0.29600 (1) obj. 52908 iterations 10
Cbc0038I Pass  35: suminf.    0.29600 (1) obj. 52908 iterations 0
Cbc0038I Pass  36: suminf.    0.29600 (1) obj. 52908 iterations 2
Cbc0038I Pass  37: suminf.    0.29600 (1) obj. 52908 iterations 3
Cbc0038I Pass  38: suminf.    0.69600 (2) obj. 52908 iterations 2
Cbc0038I Pass  39: suminf.    0.69600 (2) obj. 52908 iterations 0
Cbc0038I Pass  40: suminf.    0.48190 (5) obj. 52908 iterations 2
Cbc0038I Pass  41: suminf.    0.29600 (1) obj. 52908 iterations 9
Cbc0038I Pass  42: suminf.    1.26794 (6) obj. 52908 iterations 9
Cbc0038I Pass  43: suminf.    0.93980 (5) obj. 52908 iterations 2
Cbc0038I Pass  44: suminf.    1.18938 (5) obj. 52908 iterations 5
Cbc0038I Pass  45: suminf.    0.48190 (5) obj. 52908 iterations 4
Cbc0038I Pass  46: suminf.    1.00210 (6) obj. 52908 iterations 2
Cbc0038I Pass  47: suminf.    0.48190 (5) obj. 52908 iterations 2
Cbc0038I Pass  48: suminf.    1.20000 (6) obj. 52908 iterations 6
Cbc0038I Pass  49: suminf.    0.69600 (2) obj. 52908 iterations 8
Cbc0038I Pass  50: suminf.    0.69600 (2) obj. 52908 iterations 3
Cbc0038I Pass  51: suminf.    0.29600 (1) obj. 52908 iterations 1
Cbc0038I Pass  52: suminf.    0.20000 (1) obj. 52908 iterations 9
Cbc0038I Pass  53: suminf.    0.88358 (7) obj. 52908 iterations 9
Cbc0038I Pass  54: suminf.    0.88358 (7) obj. 52908 iterations 0
Cbc0038I Pass  55: suminf.    0.88358 (7) obj. 52908 iterations 0
Cbc0038I Pass  56: suminf.    1.25576 (8) obj. 52908 iterations 2
Cbc0038I Pass  57: suminf.    0.88358 (7) obj. 52908 iterations 2
Cbc0038I Pass  58: suminf.    0.69600 (2) obj. 52908 iterations 10
Cbc0038I Pass  59: suminf.    0.69600 (2) obj. 52908 iterations 2
Cbc0038I Pass  60: suminf.    0.29600 (1) obj. 52908 iterations 1
Cbc0038I Pass  61: suminf.    0.20000 (1) obj. 52908 iterations 14
Cbc0038I Pass  62: suminf.    1.23860 (7) obj. 52908 iterations 14
Cbc0038I No solution found this major pass
Cbc0038I Before mini branch and bound, 13 integers at bound fixed and 203 continuous
Cbc0038I Mini branch and bound did not improve solution (0.07 seconds)
Cbc0038I After 0.07 seconds - Feasibility pump exiting with objective of 53700 - took 0.04 seconds
Cbc0012I Integer solution of 53700 found by feasibility pump after 0 iterations and 0 nodes (0.07 seconds)
Cbc0038I Full problem 238 rows 335 columns, reduced to 136 rows 246 columns - 1 fixed gives 135, 245 - still too large
Cbc0038I Full problem 238 rows 335 columns, reduced to 132 rows 245 columns - too large
Cbc0006I The LP relaxation is infeasible or too expensive
Cbc0013I At root node, 0 cuts changed objective from 51900 to 53700 in 1 passes
Cbc0014I Cut generator 0 (Probing) - 0 row cuts average 0.0 elements, 2 column cuts (2 active)  in 0.000 seconds - new frequency is 1
Cbc0014I Cut generator 1 (Gomory) - 0 row cuts average 0.0 elements, 0 column cuts (0 active)  in 0.000 seconds - new frequency is -100
Cbc0014I Cut generator 2 (Knapsack) - 0 row cuts average 0.0 elements, 0 column cuts (0 active)  in 0.000 seconds - new frequency is -100
Cbc0014I Cut generator 3 (Clique) - 0 row cuts average 0.0 elements, 0 column cuts (0 active)  in 0.000 seconds - new frequency is -100
Cbc0014I Cut generator 4 (MixedIntegerRounding2) - 0 row cuts average 0.0 elements, 0 column cuts (0 active)  in 0.000 seconds - new frequency is -100
Cbc0014I Cut generator 5 (FlowCover) - 0 row cuts average 0.0 elements, 0 column cuts (0 active)  in 0.000 seconds - new frequency is -100
Cbc0014I Cut generator 6 (TwoMirCuts) - 0 row cuts average 0.0 elements, 0 column cuts (0 active)  in 0.000 seconds - new frequency is -100
Cbc0001I Search completed - best objective 53700, took 3 iterations and 0 nodes (0.08 seconds)
Cbc0035I Maximum depth 0, 12 variables fixed on reduced cost
Cuts at root node changed objective from 51900 to 53700
Probing was tried 1 times and created 2 cuts of which 0 were active after adding rounds of cuts (0.000 seconds)
Gomory was tried 0 times and created 0 cuts of which 0 were active after adding rounds of cuts (0.000 seconds)
Knapsack was tried 0 times and created 0 cuts of which 0 were active after adding rounds of cuts (0.000 seconds)
Clique was tried 0 times and created 0 cuts of which 0 were active after adding rounds of cuts (0.000 seconds)
MixedIntegerRounding2 was tried 0 times and created 0 cuts of which 0 were active after adding rounds of cuts (0.000 seconds)
FlowCover was tried 0 times and created 0 cuts of which 0 were active after adding rounds of cuts (0.000 seconds)
TwoMirCuts was tried 0 times and created 0 cuts of which 0 were active after adding rounds of cuts (0.000 seconds)

Result - Optimal solution found

Objective value:                53700.00000000
Enumerated nodes:               0
Total iterations:               3
Time (CPU seconds):             0.09
Time (Wallclock seconds):       0.09

Total time (CPU seconds):       0.10   (Wallclock seconds):       0.11

Input data

import pandas as pd

pd.DataFrame(case.gen['PMAX'])

	PMAX
GenCo0	200
GenCo1	500

case.load

	Bus1	Bus2
0	0.0	100.0
1	0.0	100.0
2	0.0	100.0
3	0.0	120.0
4	0.0	120.0
5	0.0	120.0
6	0.0	150.0
7	0.0	150.0
8	0.0	150.0
9	0.0	200.0
10	0.0	200.0
11	0.0	200.0
12	0.0	300.0
13	0.0	400.0
14	0.0	300.0
15	0.0	200.0
16	0.0	200.0
17	0.0	200.0
18	0.0	150.0
19	0.0	150.0
20	0.0	150.0
21	0.0	150.0
22	0.0	100.0
23	0.0	100.0

Model Results

model.results.unit_commitment

	GenCo0	GenCo1
0	1	0
1	1	0
2	1	0
3	1	0
4	1	0
5	1	0
6	1	0
7	1	0
8	1	0
9	1	0
10	1	1
11	1	1
12	1	1
13	1	1
14	1	1
15	1	0
16	1	0
17	1	0
18	1	0
19	1	0
20	1	0
21	1	0
22	1	0
23	1	0

model.results.power_generated

	GenCo0	GenCo1
0	100	0
1	100	0
2	100	0
3	120	0
4	120	0
5	120	0
6	150	0
7	150	0
8	150	0
9	200	0
10	150	50
11	100	100
12	150	150
13	200	200
14	150	150
15	200	0
16	200	0
17	200	0
18	150	0
19	150	0
20	150	0
21	150	0
22	100	0
23	100	0

model.results.commitment_cost

0

model.results.production_cost

43700

model.results.noload_cost

10000.0

model.results.line_power

	0
0	100
1	100
2	100
3	120
4	120
5	120
6	150
7	150
8	150
9	200
10	150
11	100
12	150
13	200
14	150
15	200
16	200
17	200
18	150
19	150
20	150
21	150
22	100
23	100

from psst.plot import line_power, stacked_power_generation

stacked_power_generation(model.results, legend=True)